Getting Started with SIMD Computation
Introduction
SIMD stands for Single Instruction Multiple Data. SIMD is a parallel computing technique where a single instruction operates on multiple data points simultaneously, improving performance for tasks involving repetitive (Instruction) calculations.
Modern CPUs (post 2016) include SIMD instruction sets that we can leverage to accelerate compute-intensive workloads. SIMD is particularly useful in the case where a GPU is not available or the particular compute problem is not well suited to be run on a GPU. SIMD also provides lower latency and wider compatibility compared to available GPGPU options.
| CPU Architecture | SIMD Instruction Sets |
|---|---|
| x86 (Intel/AMD) | MMX, SSE, SSE2, SSE3, SSSE3, SSE4, AVX, AVX2, AVX-512 |
| ARM | NEON, SVE (Scalable Vector Extension) |
| RISC-V | RISC-V Vector Extension (RVV) |
Usecases
- Image Processing
- Audio Processing
- Video Encoding/Decoding
- Machine Learning
- Financial Modelling / Scientific Computing (Weather Forecasting etc..)
Let’s Accelerate 🏎️
I will demonstrate two very simple examples:
- Matrix Multiplication
- Grayscale Conversion
Before we get started though, let’s talk about the platform and tooling we are going to work with.
Rust & SIMD
In the code, I will be using simd_portable feature which is only supported in nightly branch of rust. The motivation behind this is to ensure compilation across all the architectures with ease without any compile guards. I have already configured the project to use nightly branch of Rust, if it’s not available, rustup should automatically do the setup for you.
A very simple Hello World in SIMD is below:
#![feature(portable_simd)]
use core::simd::f32x4;
pub fn hello_simd() {
let a = f32x4::from_array([1.0, 2.0, 3.0, 4.0]);
let b = f32x4::from_array([1.0, 2.0, 3.0, 4.0]);
let result = a + b;
println!("SIMD result: {:?}", result.to_array())
}
Output:
SIMD result: [2.0, 4.0, 6.0, 8.0]
The concept here is simple, here we are using f32x4 layout, which essentially means that this data structure can hold 4 values of 32-bit floats. Unlike, scalar operations, SIMD instruction execution is truly Parallel. This is because SIMD registers in CPU are dedicated for certain type of computations only.
Matrix Multiplication
Let’s write a rust program to compute the dot product of two 256x256 matrices.
pub fn multiply_matrix_simd(
matrix_a: Vec<Vec<f32>>,
matrix_b: Vec<Vec<f32>>,
n: usize,
) -> Vec<Vec<f32>> {
let mut result = vec![vec![0.0; n]; n];
for i in 0..n {
for j in 0..n {
let mut local_sum = 0.0f32;
for k in (0..n).step_by(4) {
let a_chunk = f32x4::from_array([
matrix_a[i][k],
matrix_a[i][k + 1],
matrix_a[i][k + 2],
matrix_a[i][k + 3],
]);
let b_chunk = f32x4::from_array([
matrix_b[k][j],
matrix_b[k + 1][j],
matrix_b[k + 2][j],
matrix_b[k + 3][j],
]);
local_sum += (a_chunk * b_chunk).reduce_sum();
}
result[i][j] = local_sum;
}
}
result
}
The above example is quite straightforward, the breakdown is as follows:
- Take input of two 2D array’s -
matrix_aandmatrix_b - iterate over
M x Nloops - in
a_chunkwhich isf32x4, fill it with 4 elements from K to L + 4 in ith row. - Similarly, for
b_chunkfill it with K to K + 4 column elements fromj‘th column. - Compute element-wise product of
a_chunkandb_chunkin store the sum inresult[i][j]
Let’s also do the same matrix multiplication with A and B in 1D shape. Doing operations on 1D array will make the logic more portable to use with GPGPU programming languages (which does not support multi-dimensional arrays by default.)
fn multiply_matrix_simd_1d(matrix_a: Vec<f32>, matrix_b: Vec<f32>, n: usize) -> Vec<f32> {
let mut result = [0.0f32; 256 * 256];
for i in 0..n {
for j in 0..n {
let mut local_sum = 0.0;
for k in (0..n).step_by(4) {
let a_chunk = f32x4::from_array([
matrix_a[i * n + k],
matrix_a[i * n + k + 1],
matrix_a[i * n + k + 2],
matrix_a[i * n + k + 3],
]);
// For matrix B:
// We need the j-th column. In row-major order, the element in row k and column j
// is located at index k * n + j.
let b_chunk = f32x4::from_array([
matrix_b[k * n + j],
matrix_b[(k + 1) * n + j],
matrix_b[(k + 2) * n + j],
matrix_b[(k + 3) * n + j],
]);
// Multiply the chunks element-wise and sum their values.
local_sum += (a_chunk * b_chunk).reduce_sum();
}
result[i * n + j] = local_sum;
}
}
result.to_vec()
}
- take two parmeters
matrix_aandmatrix_bwhich are 1D representations of 256x256 matrices. - iterate over
M x N - row index is given by
i * n + kand colum index is goven byk * n + j. load k to k + 4 elements in each SIMD chunk. - Compute element-wise product of
a_chunkandb_chunkin store the sum inresult[i][j]
A primer on 1D matrix multiplication
Let,
$$ A = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{bmatrix}, \quad B = \begin{bmatrix} 12 & 11 & 10 & 9 \\ 8 & 7 & 6 & 5 \\ 4 & 3 & 2 & 1 \end{bmatrix} $$
in 1D representation, $$ A = [1, 2, 3 … 12], B = [12, 11, 10, … 1] $$
The index of the element in i‘th row is defined as:
$$
i * n + k, \\
\text{where } i \text{ is the row index, } n \text{ is the number of columns, and } k \text{ is the Offset.}
$$
Similarly,
The Index of the element in j‘th column is defined as:
$$
k * n + j, \\
\text{where } k \text{ is the row index, } n \text{ is the number of columns, and } j \text{ is the Column Index.}
$$
For example, to find the index of 6 in matrix A, the index can be calculated as:
$$
= 1 (Row Index) * 4(Columns) + 1 (Offset)
= 5
$$
Similarly, for finding the index of 10, 6 and 2 in matrix B:
$$
0 (\text{Row Index}) * 4 (\text{Columns}) + 2(\text{Column Index}) = 2 \\
1 (\text{Row Index}) * 4 (\text{Columns}) + 2(\text{Column Index}) = 6 \\
2 (\text{Row Index}) * 4 (\text{Columns}) + 2(\text{Column Index}) = 10
$$
Try out the code: Code Repository
Grayscale Conversion
Grayscale conversion is often considered a Hello World of Graphical Computing. Grayscale Conversion is essentially a reduce function, where a pixel consisting of 3 (RGB) or 4(RGBA) is reduced into 1 pixel representing the luminosity (grayness)
Utilizing SIMD, grayscale operation can be optimized. in this example, i’m using u16x8 SIMD structure, allowing us the compute the gray value for 8 pixels at a time.
pub fn to_grayscale_simd_u8(width: u32, height: u32, image_data: Vec<u8>) -> Vec<u8> {
let mut gray_pixels: Vec<u8> = Vec::with_capacity((width * height) as usize);
let r_coeff = u16x8::splat(77);
let g_coeff = u16x8::splat(150);
let b_coeff = u16x8::splat(29);
for chunk in image_data.chunks(8 * 4) {
// process 8 RGBA pixels at a time.
let mut a = [0; 8];
let mut b = [0; 8];
let mut c = [0; 8];
let mut d = [0; 8];
for (i, pixel) in chunk.chunks_exact(4).enumerate() {
a[i] = pixel[0];
b[i] = pixel[1];
c[i] = pixel[2];
d[i] = pixel[3];
}
let r_arr = u8x8::from_slice(&a).cast::<u16>();
let g_arr = u8x8::from_slice(&b).cast::<u16>();
let b_arr = u8x8::from_slice(&c).cast::<u16>();
let gray = (r_coeff * r_arr) + (g_coeff * g_arr) + (b_coeff * b_arr);
gray_pixels.extend((gray >> 8).cast::<u8>().to_array());
}
gray_pixels
}
Before we talk about *_coeff magic values in the above code, let’s consider the *luminance formula:
$$Y = 0.299R + 0.587G + 0.114B$$
However, notice that our input is a Vec<u8>. converting u8 to f32 is inefficient. alternatively, you can use an approximate integer formula (as defined in the code above) to calculate the gray pixel value without float conversion:
$$Y = (77R + 150G + 28B)\gg8$$
Let’s break down what’s happening in the code:
- I used
imagecrate to load the image from the disk and convert it to aRGBAVec ofu8. This is passed as an argument to the above function along with the image’s width and height. - declare
gray_pixelswith sizewidth x height. This will hold the grayscale pixel values. splatorsplatteringjust creates an array of structure’s length with the same value - In our case,splat(77)creates an array of 8 values of 77.- iterate over
image_data. Eachu16x8can hold 8 values ifu16. Here, we are processing 8 RGBA pixels at a time. - load the respective pixels into SIMD arrays and compute the gray pixel by multiplying with coefficients.
- bitshift the entire result array by 8. (
>> 8) and add/extend togray_pixels.
SIMD support in WebAssembly
At the time of writing this article, WebAssembly Supports 128-bit SIMD across all major browsers 1. For certain types of workloads, WebAssembly with SIMD can be much faster compared to vanilla JS implementation.
I’ve taken the above code and packaged it into a WebAssembly module using wasm-bindgen and wasm-pack.
Here’s a small demo to showcase Grayscale conversion with WebAssembly:
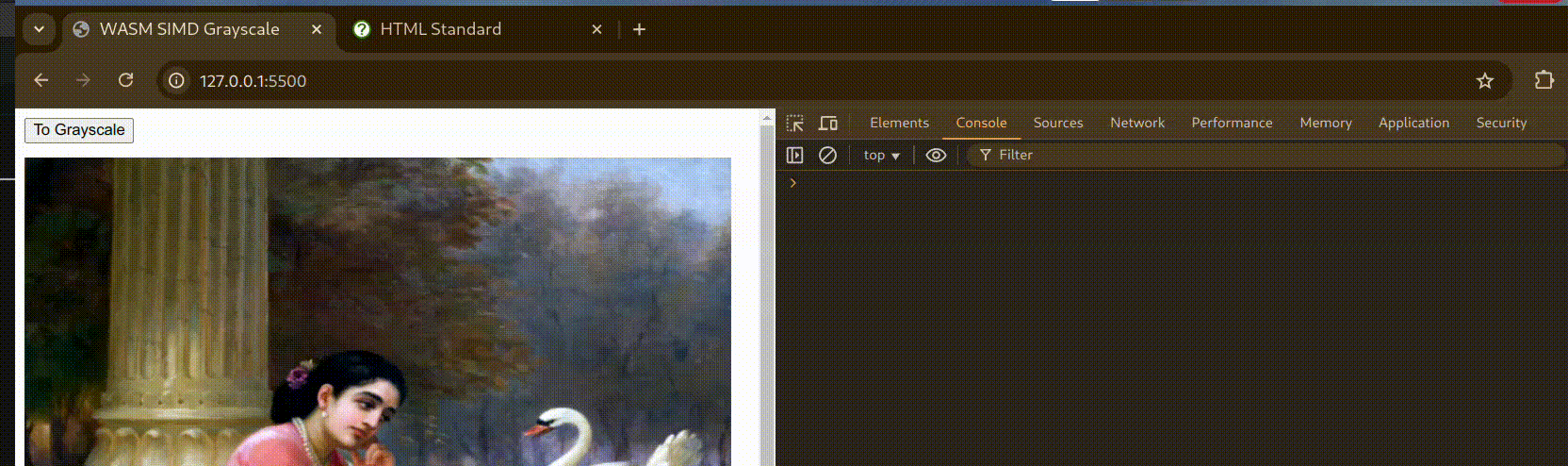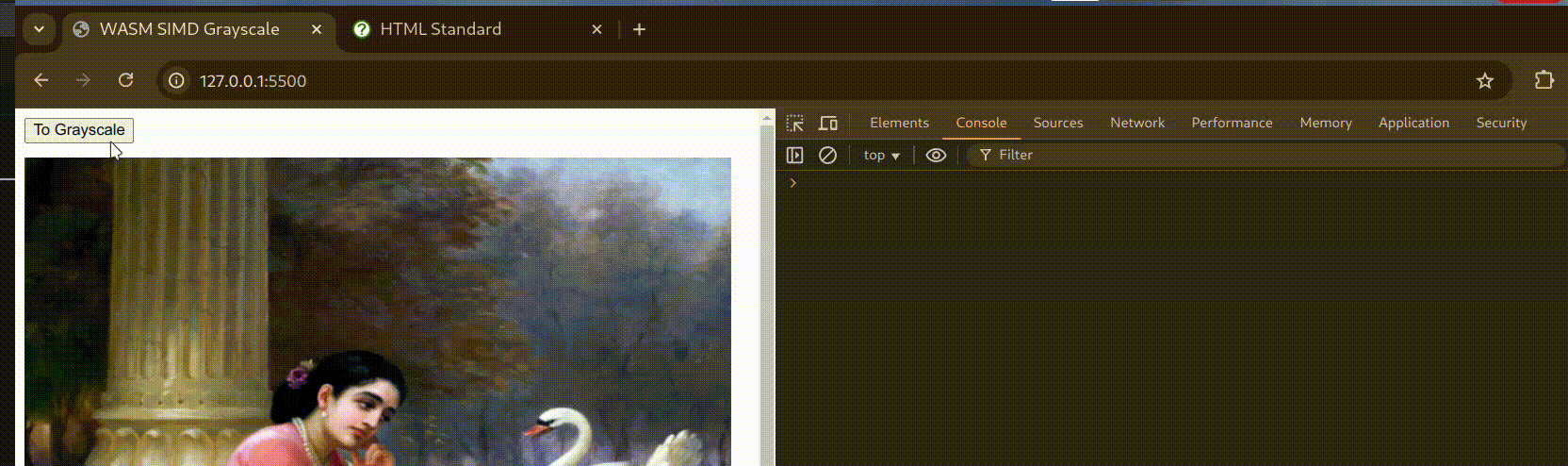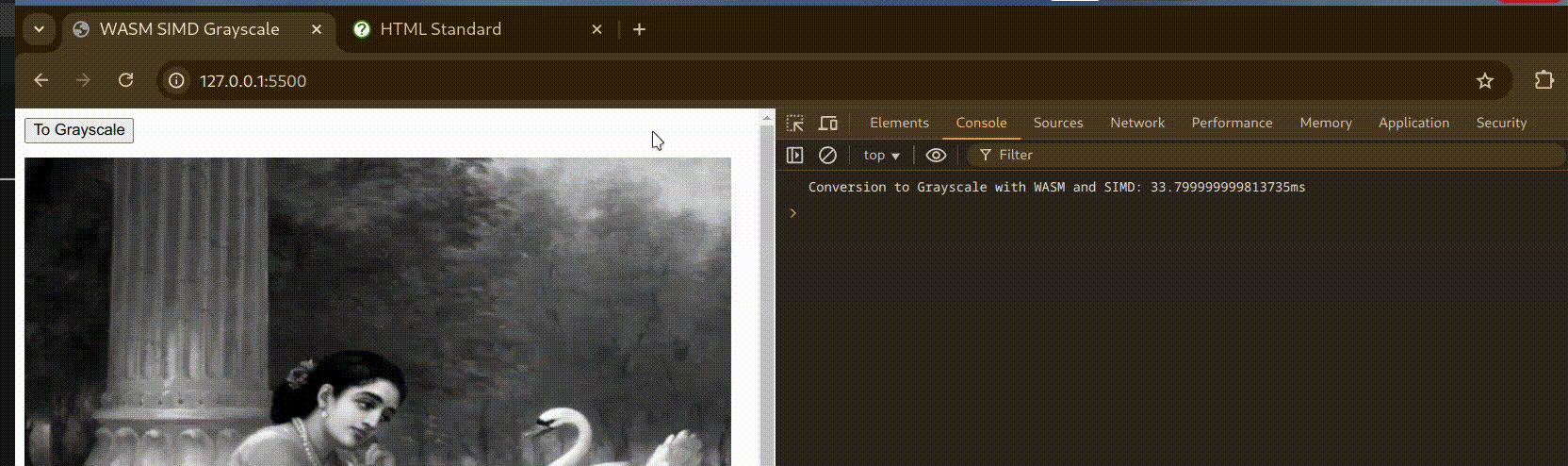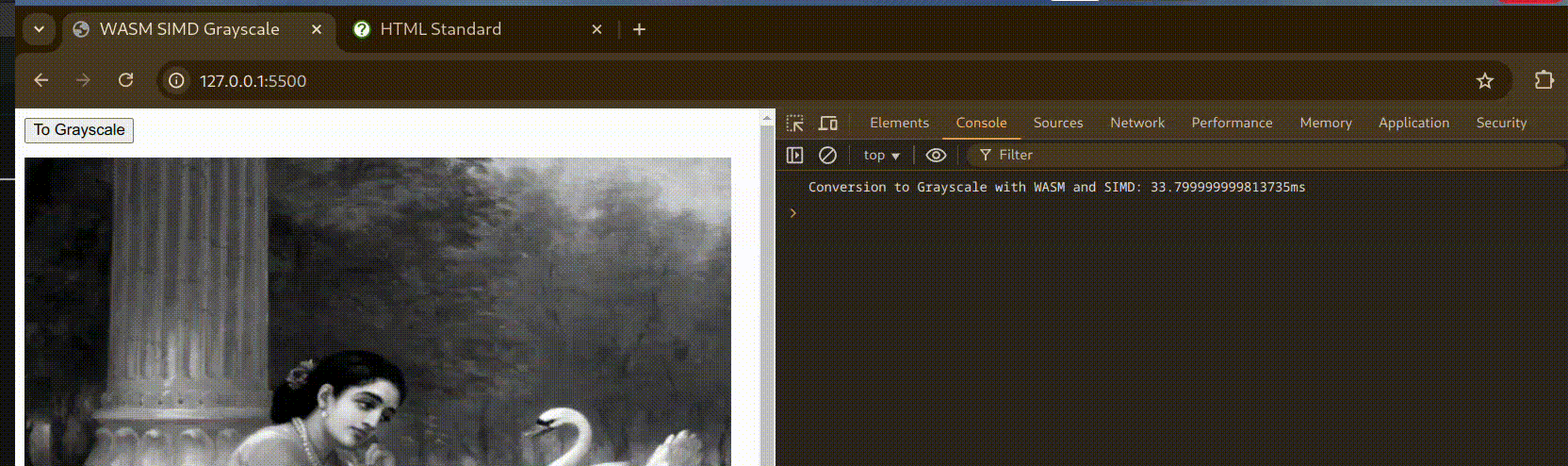
Benchmarks
These are the benchmarks for tests I have conducted. SIMD performance differs with CPU make and build. Consider the relative performance boost rather than the actual execution time differential.
matrix multiplication - scalar - time: 49.464379ms
matrix multiplication - SIMD 2D - time: 23.041549ms
matrix multiplication - SIMD 1D - time: 23.647457ms
Grayscale - scalar - time: 211.527477ms
Grayscale - SIMD - time: 8.43731ms
Conclusion
SIMD support in modern CPU’s is ubiquitous. Leveraging SIMD intrinsics in your code to optimize certain types of computations is easy thanks to easy API’s available in Rust’s portable_simd.